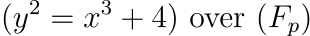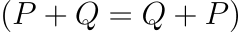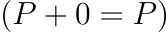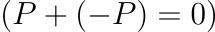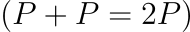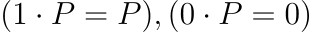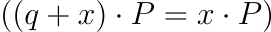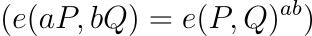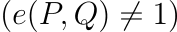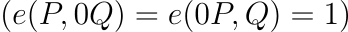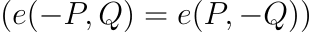EIP-2537: Precompile for BLS12-381 Curve Operations


Ethereum is stepping up its cryptographic game with EIP-2537, adding support for the BLS12-381 curve. This upgrade boosts security to 128 bits, powering faster and more efficient operations for BLS signatures, zkSNARKs, and scalable consensus mechanisms. With precompiled operations, Ethereum can now handle complex cryptographic tasks seamlessly, paving the way for a more secure and scalable future. Read on to explore how this upgrade transforms Ethereum’s cryptographic capabilities and supports next-gen blockchain applications.
TL;DR
EIP-2537 upgrades Ethereum by integrating the BLS12-381 curve, enhancing cryptographic security and adding precompiles for efficient operations like MSM and pairing checks. Here we will highlight its improvements in security, performance, scalability, and their impact on Ethereum’s consensus mechanisms.
Introduction
This Ethereum Improvement Proposal (EIP) adds support for operations over the BLS12-381 pairing-friendly curve through a dedicated precompile. The curve, designed for efficiency and security, is widely used in BLS signature schemes and zkSNARKs. Before Pectra Upgrade, Ethereum only supported BN254, a curve offering ~80-bit security, which is insufficient for long-term cryptographic robustness. This EIP, launched in the Ethereum Pectra Upgrade, provides a 128-bit security level, using BLS12-381 curve, aligning Ethereum with modern cryptographic standards and practices.
By exposing low-level cryptographic operations as precompiles, developers can avoid expensive and inefficient implementation of elliptic curve operations in Solidity or Yul. This enhances performance, encourages adoption of verifiable computation techniques, and lays a secure foundation for advanced consensus mechanisms.
Motivation
The Ethereum Virtual Machine (EVM) currently includes precompiles for elliptic curve operations on the BN254 curve, primarily used in Groth16 zkSNARK verifications. While BN254 has served its purpose in early zk-based applications, its 80-bit security level is now widely regarded as inadequate for medium to long-term cryptographic assurance.
Modern cryptographic systems require at least 128-bit security to meet regulatory standards and ensure resilience against advances in computing power, including those posed by quantum threats. BLS12-381 addresses this need by offering a pairing-friendly elliptic curve with 128-bit security, superior performance in pairing operations, and wide standardization across the blockchain ecosystem.
BLS signatures, in particular, benefit significantly from this precompile. They allow multiple signatures to be aggregated into a single compact proof, reducing bandwidth and storage requirements. Additionally, batch verification of BLS signatures drastically improves computational efficiency, especially in systems with a large number of participants, such as validators in Ethereum.
Use Case Example
Consider Ethereum's beacon chain, where each block must include attestations from potentially thousands of validators. Each attestation includes a BLS signature, and all signatures must be verified by the protocol to maintain consensus correctness. Without native support for BLS12-381 operations, verifying these signatures would require implementing complex cryptographic operations in Solidity, which is inefficient and prohibitively expensive in gas.
With EIP-2537, a smart contract can invoke the pairing precompile to efficiently validate an aggregated signature representing multiple validators. This reduces verification time from linear to constant in the number of signers (assuming proper aggregation), making real-time finality feasible and economical.
Cryptographic Specification
This section formalizes the cryptographic properties and definitions of BLS12-381 used in the precompile. It includes the base field, curve equation, extension field, group definitions, and pairing parameters.
Notation and Mathematical Definitions
Before presenting the curve parameters, we define relevant mathematical concepts:
Curve Parameters
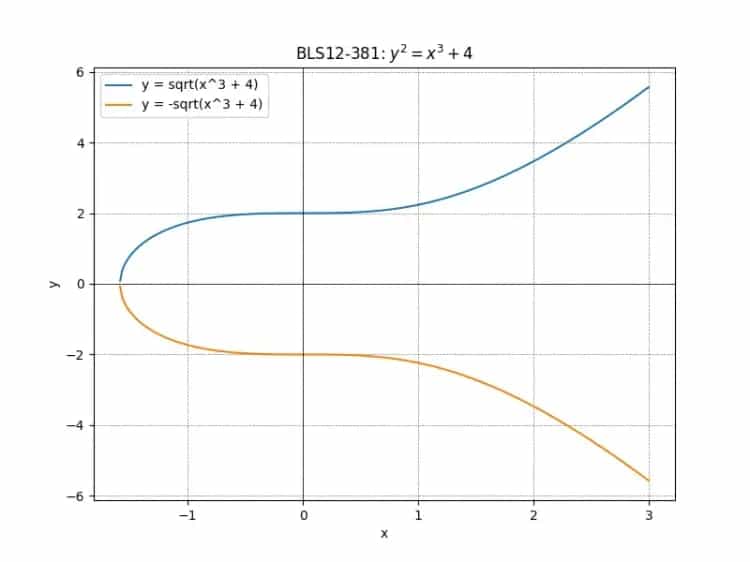
Precompile Overview
This EIP introduces seven new precompiles to the Ethereum Virtual Machine, each targeting a specific cryptographic operation over the BLS12-381 curve. These operations are designed to be accessible via low-level call instructions (CALL, STATICCALL) and have well-defined addresses within the precompile address space.
Each precompile facilitates a distinct type of operation:
This modular approach allows for optimal gas pricing and avoids overhead from composing operations manually using lower-level primitives.
Encoding Formats
To ensure interoperability and alignment with EVM expectations, all precompiles use standardized input and output encoding formats. These are designed to match 32-byte word alignment and are compatible with Solidity types such as uint256 or bytes32 arrays.
These encoding schemes are critical for validating input correctness and preventing malformed input from bypassing cryptographic constraints.
ABI Interface Behavior
Each precompile expects a well-defined binary input format and returns an equally structured output. Inputs are structured to reflect one or more operations (e.g., scalar multiplications or point pairs) and the total input length is used to infer how many operations are being performed.
Key behaviors:
This strict ABI design avoids ambiguous interpretations and ensures that clients can safely rely on precompile results.
Gas Schedule
Gas pricing is a critical design aspect of this EIP. The goal is to reflect actual computational costs while avoiding underpricing (which can lead to DoS vectors) or overpricing (which discourages usage).
Fixed-cost operations (e.g., G1ADD, G2ADD) are priced based on empirical benchmarking.
Multi-Scalar Multiplication (MSM) Discounts
MSMs benefit from Pippenger’s algorithm, which amortizes cost over multiple operations. To encourage batching, the precompile applies a decreasing discount factor (Dk) based on the number of point-scalar pairs (k).
The total gas cost is computed using:
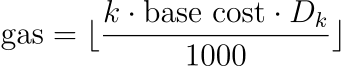
Each group (G1, G2) has its own discount table, and caps are applied for (k > 128). This pricing model encourages efficient usage while preserving determinism.
Pairing Operation
Pairing operations use a linear pricing model:
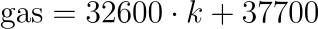
where (k) is the number of (G1, G2) pairs. The base cost reflects the setup overhead for the pairing engine.
Subgroup Checks and Security
Correctness and cryptographic security depend on ensuring that inputs reside in the correct subgroup of the elliptic curve. Small subgroup attacks can compromise security if unchecked.
The EIP enforces that:
Implementations may use optimized techniques such as cofactor clearing or endomorphism-based checks. Failing to validate subgroup membership is grounds for rejecting the input and burning all provided gas.
Security considerations also include gas-based denial-of-service protection, achieved through bounded gas formulas and avoidance of unbounded loops in implementation.
Rationale
The design decisions in this EIP balance performance, simplicity, and compatibility:
MSM as Separate Precompile
MSM is central to BLS verification. Without a dedicated precompile, verifying an aggregate signature would require calling the multiplication precompile (k) times and the addition precompile (k - 1) times. This incurs high gas due to repeated CALL overhead. A single MSM call reduces execution time and gas, while allowing use of optimized algorithms.
No Separate MUL Precompile
Single-scalar multiplication is equivalent to MSM with (k = 1). Reusing MSM infrastructure reduces implementation complexity and avoids redundant code paths. The precompile can detect (k = 1) and optimize accordingly.
Test Properties
To ensure mathematical correctness, the EIP defines a list of algebraic properties that implementations must satisfy. These properties serve as a test suite specification for both correctness and compliance.
Group Properties
Pairing Properties
These properties are foundational for cryptographic soundness and must be reflected in all client implementations.
Conclusion
EIP-2537 provides Ethereum with essential cryptographic functionality for BLS12-381, enabling modern cryptographic systems to execute efficiently and securely on-chain. It paves the way for scalable and provable consensus mechanisms, BLS-based voting systems, zkSNARK verification, and efficient signature aggregation.
The proposal defines precise interfaces, gas pricing, and correctness constraints, ensuring safety and interoperability across clients. It is a critical step toward Ethereum’s cryptographic maturity in the post-merge, proof-of-stake world.
Further Readings
Frequently asked questions
Check out most commonly asked questions, addressed based on community needs. Can't find what you are looking for?
Contact us, our friendly support helps!
What is the difference between BLS12-381 and BN254?
BLS12-381 offers 128-bit security and faster pairings, while BN254 provides only ~80-bit security, which is no longer considered sufficient for long-term cryptographic assurance.
How does EIP-2537 affect zkSNARK performance in Ethereum?
It enables efficient, low-gas verification of zkSNARK proofs using the BLS12-381 curve, making zk-based applications more scalable and secure.
Is EIP-2537 live on Ethereum mainnet?
Yes, EIP-2537 was introduced as part of the Ethereum Pectra Upgrade and is now available for use via precompiles on mainnet.

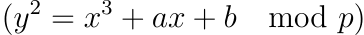 For BLS12-381,
For BLS12-381,  with specific algebraic properties used in pairing-based cryptography.
with specific algebraic properties used in pairing-based cryptography.